超时重传机制是TCP协议中最重要和最复杂的内容之一。为了提供可靠的报文传输服务,当发送方发送一个报文段后,TCP设定一个定时器,并等待确认信息。如果报文段中的数据在定时器超时之前未得到确认,TCP将认为报文段已经丢失或出现损坏,于是重传该报文段。
但是,TCP应当如何来设置定时器的超时时间呢?
显然,这个时间应该根据报文段往返发送方和接收方之间的时间来确定。然而这是一个非常有技巧性的一个问题。TCP报文段在传输中可能经过若干个网络和中间结点(如路由器),网络中复杂的变化可能导致TCP报文段往返时间RTT(Round Trip Time)存在非常大的波动,TCP必须能够适应这种情况,确定恰当的超时时间。
在TCP发展过程中RTT的确定经历了三个阶段。
采取的策略是计算RTT的加权平均值,加权因子为α,0≤α<1,公式为:
RTT=(α*Old_RTT)+((1-α)*New_Round_Trip_Sample)
超时时间一般根据RTT来确定:
Timeout=β*RTT β>1,通常推荐β=2。
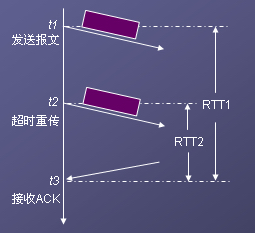
但是上述策略面临一个确认二义性问题。如下图所示:

如果t1时发送报文段,结果发现超时,于是发送方在t2时刻重传该报文段,并在t3时刻接收到对该报文段的确认。因此,我们通常会认为当前的往返时间RTT为(t3-t2)。
但是,也存在这样一个可能,那就是t3时刻收到的确认其实是t1时刻发送报文的响应,只不过由于网络延迟,导致该确认报文到达得比较晚。因此正确的往返时间应该是(t3-t1)。
然而,t3时刻收到的确认报文的确可能是对t2时刻所发送报文的确认。
这样,就出现了超时时间的二义性,即按照上述任何一种方式计算RTT都可能是错误的。
采用了Phil Karn提出的一种解决二义性的方法,也称为Karn算法,其思想是:上述计算的二义性是由于超时重传的报文段引起的,因此可以只对没有超时(也就没有二义性)的报文段的确认来重新计算往返时间RTT。
不过,这种算法对时延突然增大的情况不适用。因为时延突然增大可能导致所有报文段超时,这样,所有的报文段都需要重传。然而,由于重传的报文段不能影响RTT时间的采样,因此,超时的时间Timeout保持不变。这样,TCP就无法适应网络的延迟时间而动态调整超时时间。
采用改进的Karn算法是:如果报文段出现了重传,TCP超时的时间也会随之而延长,从而对定时器进行了补偿。常用的方式是通过一个常数因子γ计算新的时限值:
New_timeout=γ*timeout γ>1,通常γ=2。